Unit III Lesson 4

Annihilator operators, what they are what they do, the basic types.
Proof by induction of one of the annihilator types.
Find some annihilator operators for functions of various types.
Outline of the technique for solving non-homogeneous equations using annihilator method.
Example using the annihilator method for a non-homogeneous equation.

Note that any n^th order linear DE can be written with the differential operator D:

.

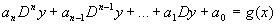More simply, we could write L(y)=g(x) for 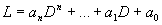where L is a linear operator.

Recall also that operators can be factored.

Example:

(D²-5D+6)y=(D-3)(D-2)y

1. Dⁿ annihilates 1,x,x²,…x^n-1.
2. Dⁿ also annihilates c₁+c₂x+c₃x²+…+c_n-1x^n-1
3. (D-A)ⁿ annihilates e^Ax, xe^Ax, x²e^Ax, …, x^n-1e^Ax
4. (D-A)ⁿ annihilates C₁e^Ax+C₂xe^Ax+C₃x²e^Ax+ …+ C_n-1x^n-1e^Ax
5. (D²-2AD+(A²+B²))ⁿ annihilates all of these:
   e^Axcos(Bx), e^Axsin(Bx), xe^Axcos(Bx), xe^Axsin(Bx), x²e^Axcos(Bx), x²e^Axsin(Bx),…,x^n-1e^Axcos(Bx), x^n-1e^Axsin(Bx)  

Take this link after you've tried it yourself.

Methods of proof

Weird humor link.

1. f(x)=x⁴-7x²+2
2. f(x)=e^2x
3. f(x)=4e^2x-xe^2x+x²e^2x
4. (harder) f(x)=9xe^2xcos(3x)-5xe^2xsin(3x) (hint: look at 5 above)
5. f(x)=Acos(kx)+Bsin(kx)

Take this link after you’ve tried these.

1. Find y_c, the solution of the homogeneous equation L(y)=0
2. Operate on both sides of the non-homogeneous equation L(y)=g(x) with an annihilator L₁ that annihilates g(x).
3. Find the general solution of the higher order differential equation L₁(L(y))=0.
4. Delete from the solution of the equation all duplicates in y_c, and form a linear combination y_p of the terms that remain. This is the ‘form’ of the particular solution to L(y)=g(x). We need the actual coefficients, so
5. Substitute this y_p and its derivatives in the original equation and solve for the coefficients, thus finding y_p.
6. The solution is y=y_c+y_p 

Take this link after you've suffered for a while yourself.

Comment: I don’t think any of the assigned problems are this tough!