y’’’+4y’=e^xcos(2x)

 Solution:

The homogeneous equation is y’’’+4y’=0 with characteristic equation m³+4m=0, so m=0 or m=+/-2i. The solution of the homogeneous equation is y_c=C₁+C₂cos(2x)+C₃sin(2x).

The equation in annihilator form is (D³+4D)y=e^xcos(2x) or annihilating the right side , we get (D²-2D+5) (D³+4D)y=0 which has characteristic equation:

(m²-2m+5)(m³+4m)=0 with roots m=0,m=2i,m=-2i,m=1+2i,m=1-2i.

The solution is y=C₁+C₂cos(2x)+C₃sin(2x)+C₄e^xcos(2x)+C₅e^xsin(2x).

All of C₁+C₂cos(2x)+C₃sin(2x) is part of the complementary solution, so y_p is of form:

y_p= Ae^xcos(2x)+Be^xsin(2x).

Therefore y_p’= -2Ae^xsin(2x)+Ae^xcos(2x)+2Be^xcos(2x)+Be^xsin(2x) and

y_p’’=-4Ae^xcos(2x)-2Ae^xsin(2x)-2Ae^xsin(2x)+Ae^xcos(2x)-4Be^xsin(2x)+2Be^xcos(2x)+ 2Be^xcos(2x)+Be^xsin(2x)

Which simplifies to:

y_p’’=-3Ae^xcos(2x)-4Ae^xsin(2x)-3Be^xsin(2x)+4Be^xcos(2x)

Differentiating again (!) yields

y_p’’’=6Ae^xsin(2x)-3Ae^xcos(2x)-8Ae^xcos(2x)-4Ae^xsin(2x)-6Be^xcos(2x)-3Be^xsin(2x)-8Be^xsin(2x)+4Be^xcos(2x)

Which simplifies to:

y_p’’’=2Ae^xsin(2x)-11Ae^xcos(2x)-2Be^xcos(2x)-11Be^xsin(2x).

Substituting back into the original equation gives:

2Ae^xsin(2x)-11Ae^xcos(2x)-2Be^xcos(2x)-11Be^xsin(2x)+

4(-2Ae^xsin(2x)+Ae^xcos(2x)+2Be^xcos(2x)+Be^xsin(2x)=e^xcos(2x)

Collecting up like terms, we have:

e^xsin(2x)(2A-11B-8A+4B)+e^xcos(2x)(-11A-2B+4A+8B)= e^xcos(2x)

So we get the system of equations:

The solution is A=-7/85, B=6/85.

The solution to our problem is y=y_c+y_p or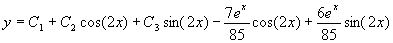

I hope I don’t have to check that answer anytime soon! Actually I did check it using Derive! AND it was correct!! (It doesn't take too many problems like this to make a dozen.)