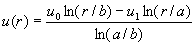Unit III Lesson 8
Boundary Value Problems
Boundary value problems: deflection (bending under its own weight) of a beam as a fourth order boundary value problem. 
Example of solving the fourth order boundary value problem, use of Cramer's rule. 
Eigenvalues and Eigenfunctions of certain types of boundary value problems. 
An example of use of Eigenvalues and Eigenfunctions applied to a structure, critical loads, 'buckling'. 
Another example of a boundary value problem. 
A 'show that' problem from thremodynamics. 
The preceding lesson was about dynamic systems that were modeled by initial
value problems. Often, however, the mathematical description of a physical
system demands that we solve a DE that has ‘boundary conditions’.
That means we know values of the function, one or more of its derivatives,
or even some linear combination of the function and its derivatives at
two or more points. Several such examples follow.

Deflection of a Beam
Many structures built by humans are constructed from girders or
beams which deflect or
distort (Shall we say bend?) under their own weight or due
to some external force. This deflection is governed by a linear
4th order DE. The diagram here shows the deflection curve of a
beam:
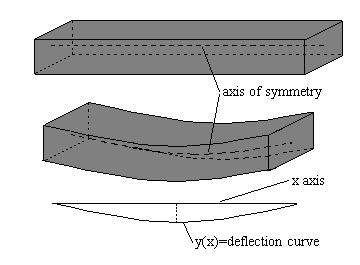
Suppose the x axis coincides with the axis of symmetry and the deflection
is positive in a downward direction. In the theory of elasticity, it is known
that the bending moment M(x) at a point x along the axis of the beam is related
to the load per unit length w(x) by the DE:

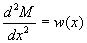
In addition, the bending moment M(x)=EIk where E and I are constants
and k is the curvature of the elastic curve. E involves the
elasticity of the beam's material (Steel is more rigid than lead, for example)
and I is the moment of inertia of a cross section of the beam about the
‘neutral axis’. The product EI is called the flexural rigidity
of the beam.
You may recall from calculus class that curvature k is given by the
formula: 
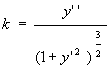 .
.
When the deflection is small y’è
0 so the denominator è 1, so
k=y’’ is used as the equation for curvature. Then M(x)=EIk
can be written M(x)=EIy’’.
Differentiating this twice gives the
DE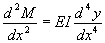 .
.
Since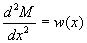 , the left side of the above
equation replaced with w(x) would
yield:
, the left side of the above
equation replaced with w(x) would
yield: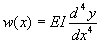 .
.

Boundary conditions associated with the equation depend on how the ends of
the beam are supported. A cantilever beam is fixed at one end
and free at the other end as the diagram shows:

For an embedded cantilever beam, the deflection y(x) must satisfy two boundary
conditions at the embedded end and two at the free end:
-
y(0)=0 since there is no deflection at this end, and
-
y’(0)=0 since the deflection curve is tangent to the x axis at this
end.
-
y’’(L)=0 (where L is the beam’s length) since the bending
moment is zero at the end
-
y’’’(L)=0 since the shear force at the end is zero.

If the beam is simply hinged on the fixed end, then y(0)=0 and
y’’(0)=0.
If the beam is embedded at both ends, there is no vertical deflection and
the line of deflection is horizontal at the endpoints, which gives boundary
conditions:
y(0)=0, y’(0)=0, y(L)=0, y’(L)=0. A picture of the situation is
given: 
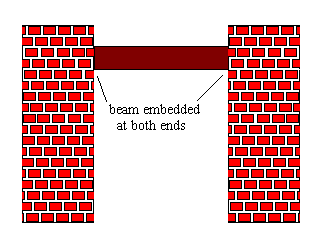
Ex1. A beam of length L is embedded at both ends, and the
constant load w0 is uniform along its length. (I.e.
w(x)=w0 for all x in the interval 0<x<L). Find the function
representing the deflection of the beam.
Take this link after trying it yourself.
Eigenvalues and Eigenfunctions
Suppose we wish to solve the BVP y’’+cy=0 with y(0)=0 and y(L)=0.
Case 1 c=0
y’’=0 is the differential equation, so y’=A, y=Ax+B and y(0)=0
forces B=0, y(L)=0 forces AL=0 hence A=0, and we have only the trivial solution
y=0
Case 2 c<0
From the characteristic equation m2+c=0 (with c<0) we get the
solutions 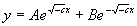 . From
the boundary values, we get the system of equations
. From
the boundary values, we get the system of equations
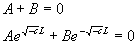

If B=-A, (from the first equation) then the second equation says
 . Since L>0
and c<0, this forces A=-B=0 and we again have only the trivial solution
y=0.
. Since L>0
and c<0, this forces A=-B=0 and we again have only the trivial solution
y=0.
Case 3 c>0 we get the solution
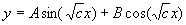 . y(0)=0 forces
B=0 and y(L)=0 means
that
. y(0)=0 forces
B=0 and y(L)=0 means
that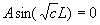 . Here either
A=0 or else
. Here either
A=0 or else 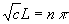 .
Solved for c, we
get
.
Solved for c, we
get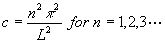 .
.
(Note if n=0, then c=0 and we already looked at that in Case 1. Hence
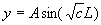 is a solution
for any A if
is a solution
for any A if 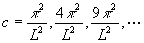 .
.

These values are called characteristic values or
eigenvalues of the equation and the
corresponding functions
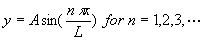
are called characteristic functions or
eigenfunctions.
Real Life Example (you don’t
have to work this one first!)
Consider a vertical column of length L hinged at both ends, with a constant
vertical compressive force (pressure) P applied to its top. The boundary
value problem governing its deflection y(x) is
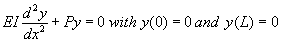
where E is a constant involving elasticity of the object’s material
and I is the moment of inertia of a cross section about a vertical line through
its centroid. Here is a picture of the situation:
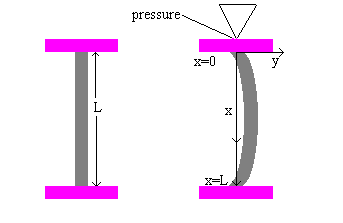
By letting c=P/EI, we have the situation described previously:
y’’+cy=0 with y(0)=0 and y(L)=0
We either have y=0 as a deflection curve or we have Case 3 where
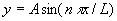 corresponding
to eigenvalues
corresponding
to eigenvalues
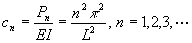
Therefore the column will buckle only if the pressure on the column is one
of the values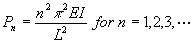 . These forces are called
critical loads.
. These forces are called
critical loads. 
The deflection curve corresponding to the smallest critical load, called
the Euler load
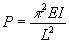 ,is
,is
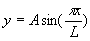 and is known as
the first buckling mode.
and is known as
the first buckling mode.
If a restraint is placed on the column at x=L/2 (half-way point), then the
smallest critical load will
be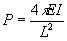 and the deflection
curve will be as in the figure shown here:
and the deflection
curve will be as in the figure shown here:

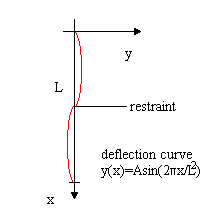
If restraints are placed at x=L/3 and x=2L/3, the critical load becomes
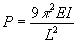 ,
,
and so forth for other values of n.
Ex2. Find the eigenvalues and eigenfunctions for the given
BVP:
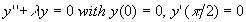
Take this link after trying it yourself.
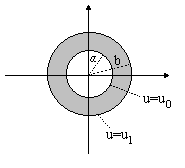
Ex3. The temperature u(r) in the circular ring shown
below is determined from the boundary value
problem: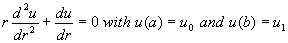 for u0 and
u1 constants.
for u0 and
u1 constants.
Show that 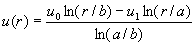
Take this link after trying it yourself.
****assignment****
Chapter 5 Section 2
Problems 1,5,9,27 Bonus for 7








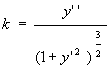 .
.
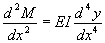 .
.
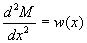 , the left side of the above
equation replaced with w(x) would
yield:
, the left side of the above
equation replaced with w(x) would
yield: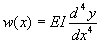 .
.


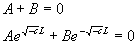
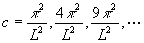 .
.
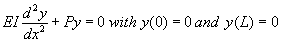

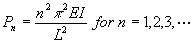 . These forces are called
critical loads.
. These forces are called
critical loads. 
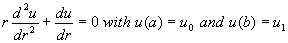 for u0 and
u1 constants.
for u0 and
u1 constants.