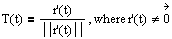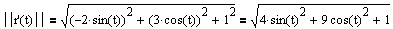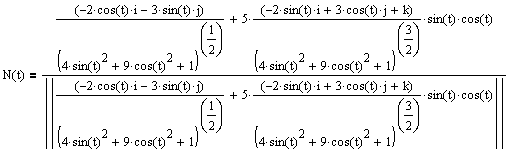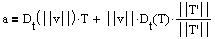12.4 Tangent Vectors and Normal Vectors

Tangent Vector and an example with graph.
Principle unit normal vector N with an example and graph.
Tangential and normal components of acceleration vector.
Proof of theorem concerning tangential and normal components of acceleration.
Example finding tangential and normal components of acceleration.
Example in R³
Example Unit tangent vector and tangent line at a point.

---

Since the velocity vector at time t points in the direction of motion, it must be tangent the the curve C traced by the vector valued function at time t. Hence this definition:

Def:   Let C be a smooth curve traced by r(t) on an open interval I. Then the unit tangent vector T(t) at t is defined as

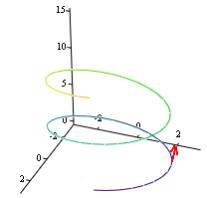
Ex 1 Find the unit tangent vector for the curve traced by the vector-valued function r(t) at the point where t = p/2. Sketch the graph and the unit tangent vector (!)

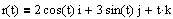
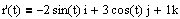
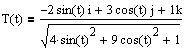
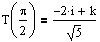
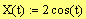
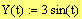
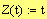
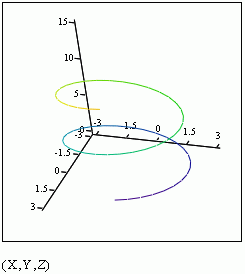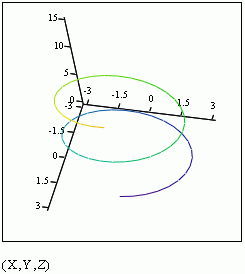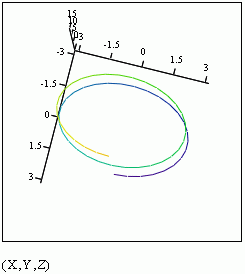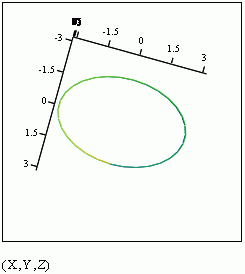
Def: Let C be a smooth curve represented by r(t) on an open interval I. If T'(t) is not 0 then the principal unit normal vector at t is defined to be

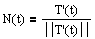
Note that the unit tangent vector points in the direction of motion at time t, and N(t) is orthogonal to T(t) and points in the direction that the object is turning. In the sketch of Ex 1 here, the principal normal vector is the purple one:

Ex 2 Find the principal unit normal vector at t = p/2

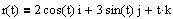
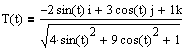
I am the first to admit this is far too ugly to do symbolically!!

 

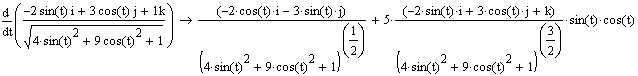
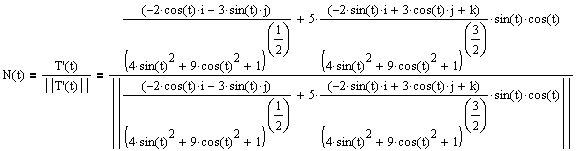
Note that cos(p/2) = 0, that helps a lot!)

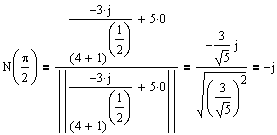
Go back and look at the purple vector on the graph; it appears to be correct! 

Note: no exam questions will be like this!! : ) 

Here are two problems where a principle unit normal vector to a vector valued function is found with reasonable detail.

For a much simpler problem look at Ex 3 pg 859 (12.4 8^th edition)

Tangential and Normal Components of Acceleration

Note we showed in Unit II Lesson 2 (Ex 5) that if ||r(t)|| is a constant, then r(t)^.r'(t) = 0. It's not much of a stretch to see that if ||r'(t)|| = c then r'(t)^.r''(t) = 0. In other words, if the speed is constant, then the tangent vector and the normal vector are orthogonal. If the object has a variable speed, this isn't necessarily so. As an example, the acceleration vector (normal) of a projectile always points down, and would only be orthogonal to the tangent vector when it is at its max imum height.

We do have a theorem about the acceleration vector and its relation to T and N:

Theorem 12.4 Acceleration Vector

If r(t) is the position vector for a smooth curve C and N(t) exists,  then the acceleration vector a(t) lies in the plane spanned by T(t) and N(t).

Proof: T = r'/||r'||= v/||v||, so v = ||v||*T

Differentiating both sides gives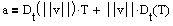

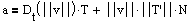
Now since a is a linear combination of T and N, it must lie in the plane spanned by T and N. The vector a is often represented as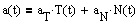

 Where a_T is the tangential component of acceleration and a_N  is the normal component of acceleration. Note a_T = D_t(||v||) and a_N = ||v||*||T'|| for v the velocity vector and T a unit tangent vector. These can be more easily computed with the following theorem:

Theorem 12.5 Tangential and Normal Components of Acceleration 

If r(t) is the position vector for a smooth curve C (that has a unit normal vector N(t)), The tangential and normal components of acceleration can be found by:

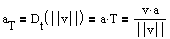
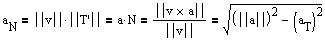
Proof: Since a lies in the plane of T and N, proj_Ta = (a^.T)T and proj_Na = (a^.N)N, so we have the middle part of the equations above. Since T = v/||v||, we have the rest of the top.

Note vxa = ||v||Tx(a_TT+a_NN) = ||v||a_T(TxT)+||v||a_N(TxN)

Note TxT = 0 (why?) so this simplifies to ||v||a_N(TxN).

Now ||vxa|| = ||(||v||a_N(TxN))|| = ||v||a_N.

Therefore a_N = ||vxa||/||v||. To get the last part, note ||a||² = a^.a.

a^.a = (a_TT+a_NN)^.(a_TT+a_NN) = (a_T)²||T||² + 2a_Ta_NT^.N + (a_N)²||N||²

Note ||T|| = ||N|| = 1, and T^.N = 0, so what we have here simplifies

to  a^.a = a_T² +  a_N². Solving for a_N gives: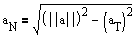

Ex 3 Find the tangential and normal components of acceleration  for the vector-valued function: (without finding T and N)

            r(t) = (cos(t) + t*sin(t))i + (sin(t) - t*cos(t))j

            v(t) = (-sin(t) + t*cos(t) +sin(t))i + (cos(t) + t*sin(t) -cos(t))j

            = t*cos(t)i + t*sin(t)j

            a(t) = (-t*sin(t)+cos(t))i + (t*cos(t) + sin(t))j

            a_T = D_t||v|| = D_t|| (-sin(t) + t*cos(t) +sin(t))i + (cos(t) + t*sin(t) -cos(t)j||  

            = D_t|| t*cos(t)i + t*sin(t) j||  

            = D_t(sqrt(t²*cos²(t)+t²*sin²(t))

            = D_t (sqrt(t²))

            = 1

For a_N, note a^.a = (-t*sin(t)+cos(t))² + (t*cos(t) + sin(t))²

                        = cos²(t) - 2t*cos(t)sin(t) + t²*sin²(t) + sin²(t) +  2t*cos(t)sin(t) + t²*cos²(t)

            = t² + 1

            a_N =sqrt((a^.a) - 1)

            = sqrt(t² + 1 - 1)

            = t

Now we can write:

            a = a_TT + a_NN

            = T +tN

Ex 4 Find T,N,a_T and a_N at t=0 for the space curve

r(t) = e^tcos(t)i + e^tsin(t)j + e^tk

            v(t) = (e^tcos(t) - e^tsin(t))i + (e^tcos(t) + e^tsin(t))j + e^tk

            v(0) = i + j + k

            ||v(0)|| = 1/sqrt(3)

            a(t) = (e^tcos(t) - e^tsin(t) - e^tcos(t) - e^tsin(t))i + (e^tcos(t) - e^tsin(t) + e^tcos(t) + e^tsin(t))j + e^tk

            a(t) = (- 2e^tsin(t) )i + (2e^tcos(t))j + e^tk

            a(0) = 2j + k

            T(t) = v/||v|| 

            = ((e^tcos(t) - e^tsin(t))i + (e^tcos(t) + e^tsin(t))j + e^tk)/||(e^tcos(t) - e^tsin(t))i + (e^tcos(t) + e^tsin(t))j + e^tk||

            = ((e^tcos(t) - e^tsin(t))i + (e^tcos(t) + e^tsin(t))j + e^tk)/(sqrt(3)e^t)

                        =(1/sqrt(3))((cos(t) - sin(t))i + (cos(t) + sin(t))j + k)

            T(0) = (1/sqrt(3))(i + j + k)

            N(t) = T'(t)/||T'(t)||

            = (1/sqrt(3))((-cos(t) - sin(t))i + (-sin(t) + cos(t))j)/||(1/sqrt(3))((-cos(t) - sin(t))i + (-sin(t) + cos(t))j)||

            = (1/sqrt(2))((-cos(t) - sin(t))i + (-sin(t) + cos(t))j)

            N(0) = (1/sqrt(2))(-i + j)

so at t = 0, we have

            a_T = a(0)^.T(0) = sqrt(3)

                        a_N =  a(0)^.N(0) = sqrt(2)  

Ex 5 Find a unit tangent vector and the parametric form of the equation of the line tangent to the curve  r(t) = <2sin(t),2cos(t),4sin²(t)> at point P(1,sqrt(3),1)  

r'(t) = <2cos(t),-2sin(t),8sin(t)cos(t)> and at P(1,sqrt(3),1), the t value of the function would be t = p/6

r'(p/6) = <sqrt(3),-1,2sqrt(3)> and T(p/6) = r'(p/6)/||r'(p/6)|| = (1/4)(<sqrt(3),-1,2sqrt(3)>).

Note we can use direction numbers sqrt(3),-1, and 2sqrt(3), so at the point P we get parametric equations x = sqrt(3)t + 1, y = -t + sqrt(3), z = 2sqrt(3)t + 1

---

Assignment: Read example 7 page 865, 12.4 # 3, 5, 7, 9, 15, 21, 25, 27, 39, 41, 45, 49, 55, 57, 73